本文共 3553 字,大约阅读时间需要 11 分钟。
深度网络 DNN 的性能为何如此之强,是深度学习理论中的一大难题。对于此的研究有 2 个层次:
这里的第1层次,涉及的概念是损失平面(loss surface),即损失函数(loss function)随参数的变化情况。
训练网络的目标是最小化损失函数。从前的看法是,通过梯度下降方法在大多数情况下只能到达局部极小值点(local minimum)。如果希望到达全局极小值点(global minimum),往往会是个NP-hard问题,即,很难保证实现这一目标。
而《The Loss Surfaces of Multilayer Networks》(https://arxiv.org/abs/1412.0233)证实了这一点。通过与理论物理中的自旋玻璃(spin glass)模型类比,研究人员发现,网络越大,越难通过训练到达全局极小值点。
但是,这里的关键是,研究人员同时发现,网络越大,局部极小值点和全局极小值点的差距会越小。换而言之,此时到达局部极小值点已足够好。
因此,网络越大,训练的过程会越简单,越稳定,因为到达任意一个局部极小值点就足够好了。我们在本书第 2 章结尾的例子中也看到了这一现象。如果计算资源充分,应使用尽可能大的网络。
根据《Identifying and attacking the saddle point problem in high-dimensional non-convex optimization》(https://arxiv.org/abs/1406.2572),真正阻碍收敛的往往是鞍点(saddle point),而不是局部极小值点。本书第 3 章也曾对此介绍。
对于第 2 层次,在 2016 年底的著名论文是《Understanding deep learning requires rethinking generalization》(https://arxiv.org/abs/1611.03530)。研究人员在实验中发现,即使将训练数据的标签和图像设置为噪音,深度网络也会若无其事地完全学会所有训练数据(此时就相当于完全死记硬背,因为标签和图像是随机设置的没有意义的数字),如下图所示。
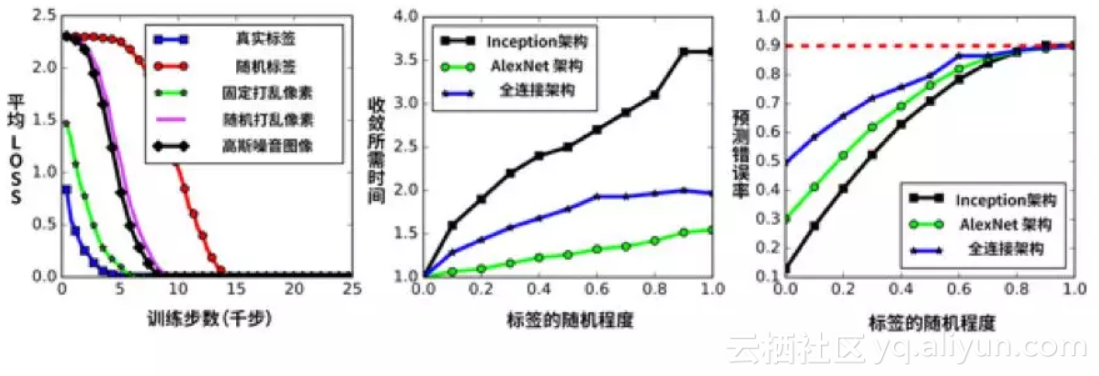
如图 (a) 所示,使用随机标签(红色),将图像像素按某固定的乱序打乱(绿色),随机打乱(粉红色),使用完全随机的图像(黑色),最终的训练误差都可降到 0。
如图 (b) 所示,随着标签的随机程度增加,训练速度会越来越慢,但不同架构的变慢程度与架构的性能并没有关联性。
如图 (c) 所示,随着标签的随机程度增加,网络的预测错误率也会随之增加,但不同架构的错误增长情况同样是相近的。
此外,研究人员还实验了使用核方法(kernel trick)的线性模型(相当于浅层神经网络),它可直接通过计算实现 0 训练误差,我们希望了解它的泛化性能如何。研究人员发现,它在 MNIST 的测试错误率只有 1.2%(这证明 MNIST 确实太简单)。而对于 CIFAR-10 问题,如果预先做高斯模糊处理,可实现 46% 的错误率;如果预先用 32000 个随机卷积核处理,错误率就会降到 15% (注意这还没有使用数据增强,因为否则训练时的计算量太大),已经接近早期深度神经网络的性能。
这说明,如果使用合理的训练方法,并加入图像预处理,浅层神经网络的泛化能力实际也不错。或许,这也说明,图像分类其实本来就并非那么难。
在 2017 年的另一篇热议论文是《Opening the Black Box of Deep Neural Networks via Information》(https://arxiv.org/abs/1703.00810)。它发现,网络的训练可分为两个阶段:
如下图所示,网络的高层(层 5)在一开始与数据和标签的信息相关度都很低。随着训练的进行,它与标签的信息相关度不断提高(因为最终需要给出标签),而与数据的信息相关度先提高(从A到C)后降低(从C到E),说明它一开始是着眼于输入数据,后来就逐渐脱离了输入数据,转为关注更高层次的规律。
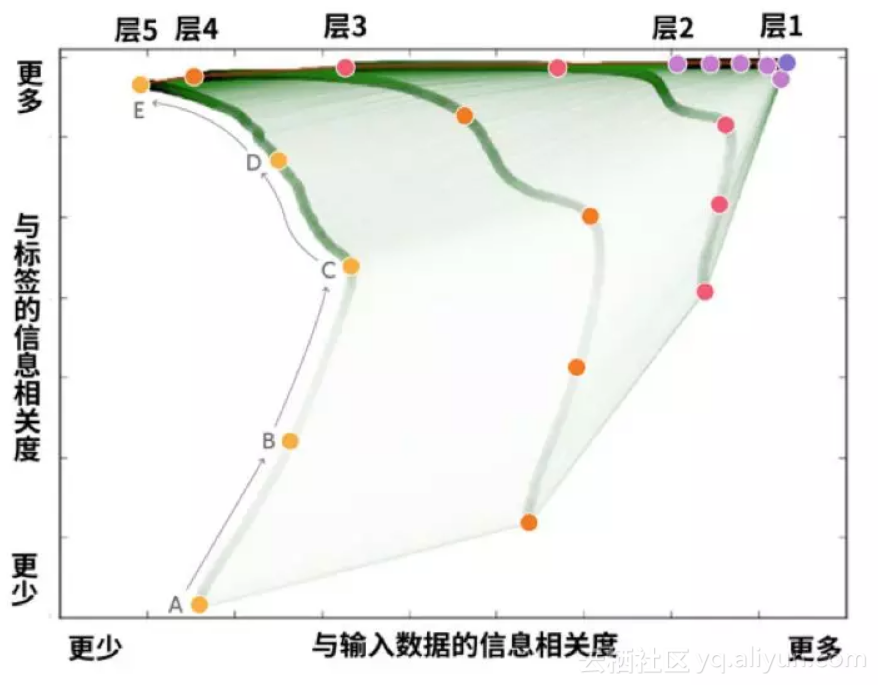
这听上去很有趣,就像我们平时说的“先把书读厚,再把书读薄”,引来了许多科技媒体争相报道。Hinton 也表示,这是近年来少有的突破,是真正原创的想法。
不过,在本书写作的时候,也有研究人员认为这篇文章有问题,因为其中的网络架构令人生疑地原始,是全连接网络,而且使用 tanh 和 sigmoid 激活,而非 ReLU 激活。经过实验,使用 ReLU 激活后,这些有趣的现象似乎就消失了(https://openreview.net/forum?id=ry_WPG-A-¬eId=ry_WPG-A-)。这不代表这个研究没有价值,不过说明事情可能没这么简单,需要用更多的模型检验。
说起这个问题,目前部分AI论文的作者会回避对于自己不利的实验结果,值得读者注意。例如,如果某个模型只发布了在简单数据集上的性能(如 MNIST),那可能是因为这个模型在更复杂数据集(如 CIFAR-10)的性能不佳,论文的作者不好意思说出来。
此外,目前也有研究人员试图从物理的角度解释深度学习的有效性,有能力的读者可参阅《Why does deep and cheap learning work so well?》(https://arxiv.org/pdf/1608.08225)。
简单地说,机器学习希望学会统计分布,统计分布在物理上来自哈密顿量(Hamiltonian)。如果哈密顿量具有简单的形式(例如,是阶数低的多项式),或明确的对称性,或存在简单的有效理论(effective theory),就会适合于神经网络的学习。此外,我们宇宙存在明显的层次结构(hierarchical structure),这也很适合于深度网络的训练和运作。不过,这仍然是停留在想法层面,研究人员仍未找到严格的理论模型。
最后,在 2017 年 12 月的一篇有趣的文章是《Deep Image Prior》(https://dmitryulyanov.github.io/deep_image_prior)。它让一个深度卷积网络去学习复制被破坏的图像(如,加入噪点的图像),发现这个网络会自动先学会重建图像。
例如,给定一幅被破坏的图像 x,具体过程如下:
这意味着,深度卷积网络先天就拥有一种能力:它会先学会x中“未被破坏的,符合自然规律的部分”,然后才会学会 x 中“被破坏的部分”。例如,它会先学会复制出一张没有噪点的 x,然后才会学会复制出一张有噪点的 x。
换而言之,深度卷积网络,先天就了解自然的图像应该是怎样的。这无疑来自于卷积的不变性,和逐层抽象的结构。
Deep Image Prior 的重要特点是,网络由始至终,仅使用了被破坏过的图像x作为训练。网络没有看过任何其它图像,也没有看过正常的图像,但最终效果依然颇为不错。这说明自然图像的局部规律和自相似性确实很强。
请看下图,最左边是带瑕疵的图像 x,它经过 JPEG 压缩,有很多压缩瑕疵。网络的目标是学会输出它。在 100 次迭代后,网络学会了输出模糊的形体。在 2400 次迭代后,网络学会了输出清晰光滑的高质量图像。在 50000 次迭代后,网络才学会了输出带瑕疵的图像 x。
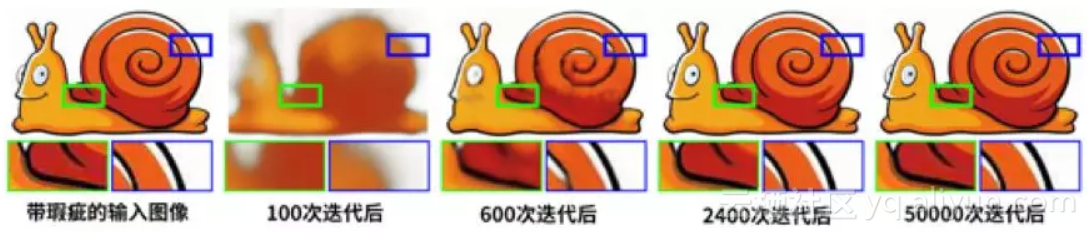
而下图是将图像由部分像素重建。可见,深度卷积网络很擅长处理不断重复的纹理,效果比传统方法更佳。

原文发布时间为:2018-06-3
本文作者:彭博
本文来自云栖社区合作伙伴“”,了解相关信息可以关注“”。
转载地址:http://dlhsa.baihongyu.com/